Regression oder einfache Regression ist eine Analysemethode, die von der Finanzwelt und verwandten Disziplinen weit verbreitet wird. Möchten Sie investieren? Führen Sie eine Regressionsanalyse durch. Möchten Sie Warenpreise untersuchen? Regression ist die Lösung. Sie können von der Regressionsanalyse profitieren, wenn Sie Entscheidungen treffen, die sich auf die Finanzen Ihres Unternehmens auswirken werden.
In diesem Artikel wird eine einfache Definition der Regressionsanalyse gegeben. Die wichtigsten Arten der Analyse und ihre Beispiele werden aufgelistet. Ihre Vorteile werden dargelegt, damit Sie verstehen, warum Sie diese Analyse verwenden sollten. Warten Sie also nicht länger und fangen Sie an, den Artikel zu lesen.
Was ist eine Regressionsanalyse?
Die Regressionsanalyse ist eine Forschungsmethode, die verwendet wird, um die Verbindungen zwischen einer oder mehreren unabhängigen Variablen und einer abhängigen Variablen zu messen.
Sie hilft dabei, den Wert einer abhängigen Variablen zu schätzen, indem sie die Veränderungen untersucht, die um sie herum auftreten. Dies ist in der Regel objektiv, da es sich um mathematische Daten handelt. Sie wird zusammen mit der Datenvisualisierung mit geeigneten Tools verwendet und zeigt gekrümmte oder gerade Linienmuster von Datenpunkten auf. Somit haben Unternehmen mithilfe dieser Analysemethode Vorabinformationen über zukünftige Situationen.
Arten der Regressionsanalyse & Beispiele
Bei der Durchführung der Datenanalyse können Sie verschiedene Methoden nutzen. Jede Methode enthält einzigartige Berechnungen und bietet effektive Einblicke in verschiedene Themen.
Sie können immer von verschiedenen Arten der Datenanalyse profitieren, wie z.B. Cluster-Analyse und Conjoint-Analyse. Die Regressionsanalyse wird jedoch immer Ihre erste Referenz für statistische Modellierung sein. Im Folgenden werden Beispiele für jede Art von Regressionsanalyse genannt:

Arten der Regressionsanalyse
1. Lineare Regressionsanalyse
Einfache lineare Regression ist eine statistische Methode zur Modellierung der Beziehung zwischen einer einzelnen unabhängigen (Prädiktor-) und einer abhängigen Variablen. Hier wird eine lineare Beziehung angenommen. Das bedeutet, dass bei einer Veränderung der Prädiktorvariablen auch eine entsprechende Veränderung in der abhängigen Variablen vorliegt. Der Zweck dieser Methode ist es, Vorhersagen über die abhängige Variable zu treffen. Sie wird auch zur Vorbereitung auf komplexere Regressionsmodelle verwendet.
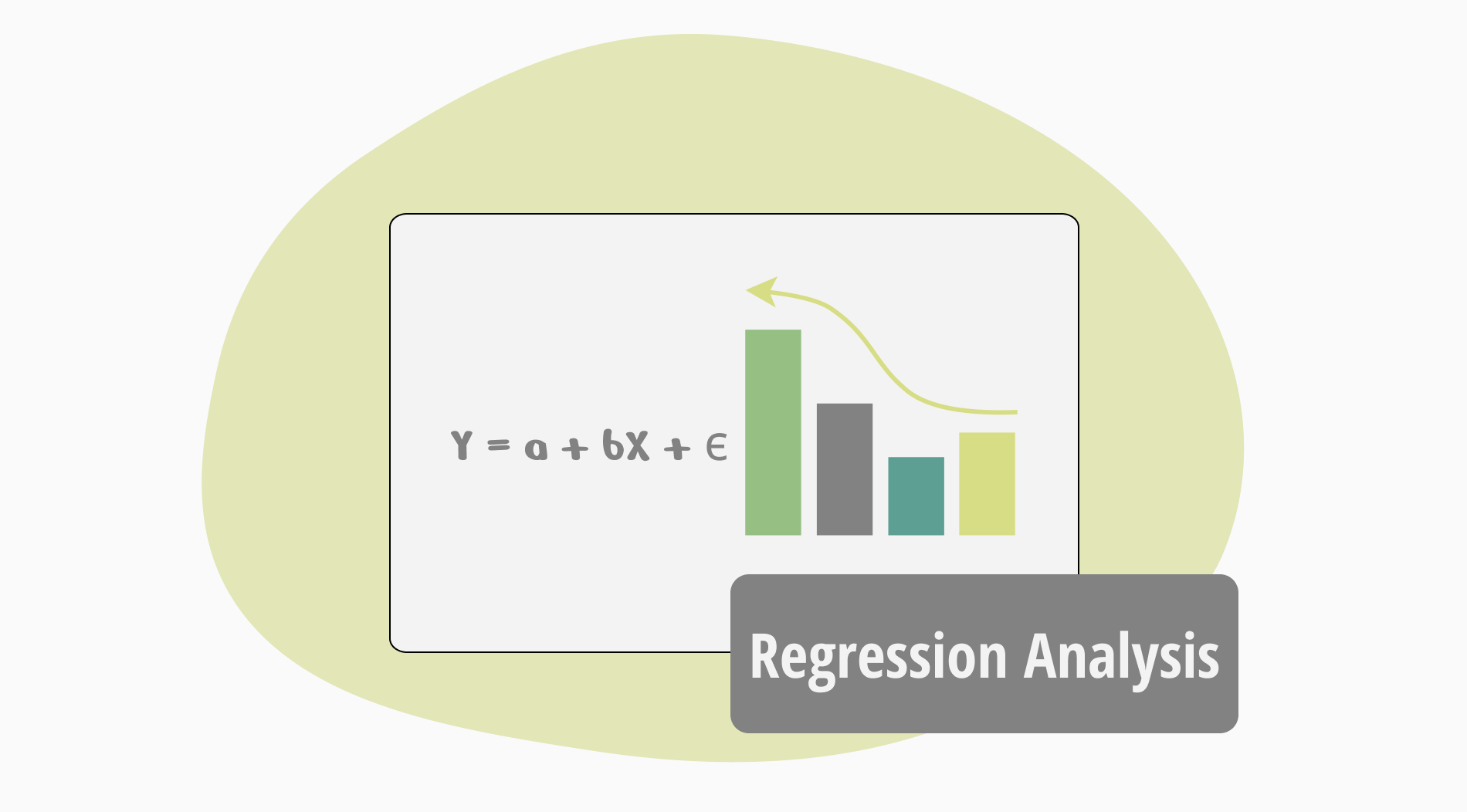
Regressionsformel:
Y = a + bX + ϵ
Y – Abhängige Variable
X – Unabhängige Variable
a – Schnittpunkt
b – Steigung
ϵ – Residuum (Fehler)
Beispiel: Sie möchten ein Modell erstellen, um den Laden zu finden, der Ihren Zwecken entspricht und die Ladenpreise zu schätzen. Nehmen wir an, ein bestimmter Ladenpreis ist eine abhängige Variable. Dieser beträgt X Dollar. Die unabhängige Variable ist die Gebäudefläche. Sie analysieren die Beziehung zwischen den beiden Variablen. Mit der besten Anpassungslinie machen Sie die Ladenpreise im Modell sichtbar und vorhersagbar.
2. Multiple Regressionsanalyse
Bei der Multiplen Regressionsanalyse werden mehrere Variablen zum einfachen linearen Regressionsmodell hinzugefügt. Das Ziel hierbei ist es, den Koeffizienten jeder Variablen mit einer linearen Kombination zu finden. Dadurch können Sie verstehen, wie sich gleichzeitige Veränderungen in verschiedenen Prädiktoren auf die abhängige Variable auswirken.
Beispiel: In dieser Art der Analyse fügen Sie die Merkmale zu dem oben gesuchten Laden hinzu. Zum Beispiel kann er einen Keller, einen Parkplatz, einen Dachboden usw. haben. Wenn architektonische Merkmale hinzugefügt werden, beobachten Sie, ob sich die Ladenpreise ändern.
3. Logistische Regressionsanalyse
Diese Methode ist nicht-linear und wird verwendet, um die Wahrscheinlichkeit von Ereignissen mit einer oder mehreren Variablen abzuschätzen. Hier wird eine logische binäre Variable verwendet, d.h. ja/nein, wahr/falsch. Die Wahrscheinlichkeiten werden auf eine Funktion abgebildet, die als Sigmoid-Kurve bekannt ist. Das heißt, Kombinationen werden in Wahrscheinlichkeiten zwischen 0 und 1 umgewandelt.
Beispiel: Sie möchten die Wahrscheinlichkeiten berechnen, ob Ihre Kunden Ihr neues Produkt wählen werden. Zunächst erstellen Sie einen Datensatz, der die demografischen Merkmale und Einstellungen Ihrer Kunden zu den Produkten enthält, die Sie zuvor veröffentlicht haben. Mit der für diese Daten geeigneten logistischen Modellierung können Sie die möglichen Ergebnisse in binärer Form erlernen. Sie können auch das Kundenverhalten mit Narrativanalyse weiter analysieren.
4. Polynomiale Regressionsanalyse
Dies ist eine Regressionsmethode, die verwendet wird, um Variablen in einer nicht-linearen Beziehung zu modellieren. Sie bietet eine flexiblere Datenanalyse. Die polynomiale Regressionsanalyse ist Ihre Referenzquelle, insbesondere wenn Sie ein schlecht funktionierendes Modell erstellen und feststellen, dass es nicht mit den tatsächlichen Werten übereinstimmt. Sie ermöglicht es Ihnen, die beste Anpassungslinie zu prognostizieren, indem Sie den Mustern der Datenpunkte folgen.
Beispiel: Sie möchten analysieren, ob ein Lebensmittelprodukt je nach Jahreszeit mehr verkauft wird. Sie sammeln Daten zu den von Ihnen verkauften Lebensmittelprodukten nach Monaten und Jahreszeiten. Es ist jedoch offensichtlich, dass keine lineare Beziehung besteht, daher wenden Sie die polynomiale Regressionsanalyse an. Mit der polynomen Kurve können Sie saisonale Schwankungen genauer vorhersagen. So wird das Umfeld für die Strategien des neuen Marktes vorbereitet.
Vorteile der Regressionsanalyse
Wie bereits erwähnt, misst die Regressionsanalyse den Einfluss unabhängiger Variablen auf abhängige Variablen. Unternehmen nutzen diese Analyse, um Vorhersagen zu vielen verschiedenen Themen zu treffen. Auf diese Weise erhalten Sie einen bewussteren und objektiveren Entscheidungsmechanismus. Im Folgenden finden Sie die wichtigsten Vorteile, um Ihnen eine Vorstellung zu geben:
Vorteile der Regressionsanalyse
- Bessere Planung und Prognose: Regressionsmodelle können Trends visuell darstellen, damit Sie bessere Daten für die Planung haben.
- Hypothesentestung: Wie bei jeder Art von Analyse kann die Regressionsanalyse verwendet werden, um eine bestimmte Hypothese zu bewerten.
- Flexibilität: Mit linearen und nicht-linearen Regressionsmodellen sind Lösungen für verschiedene Datentypen und Forschungsfragen einfacher zu finden.
- Effizienz: Es bereitet Ihr Unternehmen auf praktischere Lösungen und effektivere Methoden vor.
Häufig gestellte Fragen zur Regressionsanalyse
Willkommen bei den FAQs zur Regressionsanalyse! Hier können Sie weitere Informationen zu diesem Thema erhalten oder Ihr Wissen vertiefen.
Die Regressionsanalyse gibt Aufschluss über die Veränderungen, Beziehungen und Ordnungen zwischen den Variablen. Dabei wird eine abhängige Variable zugrunde gelegt, und die Analyse versucht, die abhängige Variable und ihre Verbindungen zu anderen unabhängigen Variablen zu verstehen.
Der Anwendungsbereich der Regressionsanalyse ist breit gefächert und kann an viele Situationen angepasst werden. Unternehmen nutzen sie vor allem in der Marktforschung, um das Kundenverhalten zu verstehen und Marktstrategien zu entwickeln. Außerdem nutzen Unternehmen sie, um ihre Finanzlage, Aktien, Inflation oder Zinssätze zu untersuchen und zu berechnen.
Sie ist besonders nützlich, wenn es darum geht, zukünftige Trends und wirtschaftliche Situationen anhand historischer Daten zu verstehen. Darüber hinaus wird sie auch in der Betriebsphase, bei Feldstudien, in der Sozialforschung, im Gesundheitswesen und im Sportbereich eingesetzt.
Natürlich führt man sie zuerst durch, wenn man Daten analysieren und Muster aufdecken will. Man führt sie durch, um eine Situation vorherzusagen und Möglichkeiten aufzudecken. Man führt sie durch, um ein Datenmodell zu bewerten, es zu testen und seine Nützlichkeit zu erfahren. Oder Sie haben eine Hypothese und verwenden die Regressionsanalyse, um sie zu testen.
Regression und Korrelation sind zwei unterschiedliche statistische Verfahren. Sie untersuchen beide die Beziehungen zwischen Variablen, unterscheiden sich aber durch ihren Zweck. Der Hauptunterschied zwischen Regression und Korrelation besteht darin, dass sich die Regression auf die Vorhersage und Modellierung konzentriert.
Sie untersucht die Aktion und Reaktion einer unabhängigen Variablen mit einer oder mehreren unabhängigen Variablen. Bei der Korrelation hingegen wird die lineare Beziehung von Variablen zueinander untersucht. Dadurch lassen sich Zusammenfassungen leichter erstellen und Ursache-Wirkung-Situationen besser verstehen.
Fazit
Zusammenfassend ist die Regressionsanalyse in diesem Artikel hauptsächlich für Unternehmen erwähnt. Obwohl die Feinheiten und Merkmale der Regressionsdatenanalyse nicht auf diesen Artikel beschränkt sind, wurden Ihnen ihre Hauptbestandteile und statistische Bedeutung gezeigt.
Die hier genannten Teile sind die Definition der Regressionsanalyse, Regression und multiple Regression, andere nichtlineare Typen und Beispiele sowie schließlich ihre Vorteile. Nachdem Sie diesen Artikel gelesen und die Welt der Statistik verstanden haben, ist die Vorhersage der Zukunft in der realen Welt einen Schritt näher.
Atakan ist ein Inhaltsverfasser bei forms.app. Er recherchiert gerne in verschiedenen Bereichen wie Geschichte, Soziologie und Psychologie. Er beherrscht Englisch und Koreanisch. Seine Expertise liegt in der Datenanalyse, Datenarten und -methoden.
Beginnen Sie noch heute mit forms.app
- Unbegrenzte Ansichten
- unbegrenzte Anzahl von Fragen
- unbegrenzte Benachrichtigungen